★ 사교육비 관련 5개년 데이터 출처(Kosis)를 이용하여 공부해보겠습니다.
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/NeatyNut/csv/main/%ED%95%99%EA%B5%90%EA%B8%89%EB%B3%84_%EC%82%AC%EA%B5%90%EC%9C%A1%EB%B9%84_%EC%B4%9D%EC%95%A1_20231122115229.csv', encoding='cp949')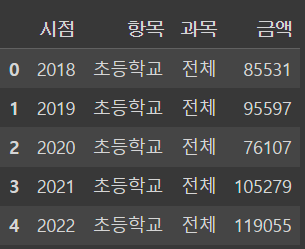
★ 링크는 개인 깃허브이므로 연결이 안될 수도 있습니다
1. 레이블 데이터 전처리
★ Why? "머신러닝 모델은 문자 데이터를 인식하지 못하기 때문"
★ ★ 문자 데이터를 가진 컬럼 뽑기 (pandas에선 'object'인 컬럼들을 뽑는 법)
cols = df.select_dtypes("object").columns # 문자열 데이터의 컬럼명들을 뽑아낸다.
1) 레이블 인코딩 (한 컬럼의 문자열들을 0~N의 숫자에 대응)
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder() # 클래스 객체로 선언
for col in cols : # object컬럼마다 호출
le.fit(df[col]) # 데이터 인풋
df[col] = le.transform(df[col]) # 변환한 데이터를 df에 다시 담아준다
#df[col] = le.fit_transform(df[col]) 로 fit, transform을 한줄로 해결 가능하다.
★ 항목 확인하는 법(단, 마지막으로 인코딩한 것만 저장되기에, for구문에 같이 두어서 보관하는 것이 좋음)
le.classes_
★ ★ 데이터 원상복구(마지막으로 인코딩한 것만 가능)
le.inverse_transform(df[col])
★ ★ [주의] 보다시피, le.classes_를 가져다 썻을 것으로 보이기에 강제적으로 마지막 작업했던 "과목"이 아닌 "항목"칼럼을 쓸지라도, '초등학교' ~ '고등학교'로 변환되진 않는다.(개수가 달랐다면 아마 오류 발생 했을 것)
le.inverse_transform(df["항목"])
2) 원핫 인코딩
(1) sklearn을 활용하는 방법!
from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder(sparse_output=False) # 생략 시 "sparse_output=True"로 matrix반환, "sparse_output=False"시 array로 반환
ohe.fit(df[cols]) # 데이터 인풋
cat = ohe.transform(df[cols]) # 변환한 array반환
df_cat = pd.DataFrame(cat, columns=ohe.get_feature_names_out()) # 데이터프레임화
df = pd.concat([df, df_cat], axis=1) # 옆으로 합치기
df = df.drop(cols, axis=1) # 기존 컬럼 삭제
★ 단, 클래스 선언시 들어간 sparse_output은 버전에 따라 sparse라는 파라미터일 수 있다.
★★ 원핫코딩된 항목들을 확인하는 두가지 방법
ohe.categories_
ohe.get_feature_names_out() # 컬럼명_항목1, 컬럼명_항목2 로 구성된 array
(2) pandas을 활용하는 방법! ★sklearn 대비 매우 쉬우나, 상황에 따라 sklearn으로 해야할 때가 필요하니 둘다 숙지!
df = pd.get_dummies(df)
df
2. 수치형 데이터 스케일링
★ Why? "데이터마다 스케일이 다르면 정확도가 떨어질 수 있어, 머신러닝 성능개선을 위해 필요함"
★ ★ 숫자형 데이터를 가진 컬럼 뽑기 (pandas에선 'int'나 'float'인 컬럼들을 뽑는 법)
cols = df.select_dtypes(["int", "float"]).columns
★ ★ ★ 개념 정리
- Standardization (표준화) : 평균0, 분산1로 스케일링(정규분포화)
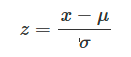
- Normalization (정규화) : 가장 작은 값이 0, 가장 큰 값이 1로 변환 (0~1 사이의 수직선에 모든 값을 놓이게 하는 개념)
(순서가 아닌 좌표의 의미, 예시로 [1,3,4]가 있을 때 3은 중앙이 아닌, 2/3 위치에 있다.)

1) StandardScaler = Standardization (표준화)
from sklearn.preprocessing import StandardScaler
SS = StandardScaler() # 클래스 선언
SS.fit(df[cols]) # 데이터 인풋
df[cols] = SS.transform(df[cols]) # 변환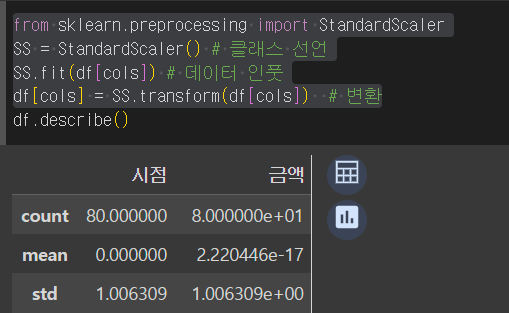
2) MinMaxScaler = Normalization (정규화)
from sklearn.preprocessing import MinMaxScaler
MM = MinMaxScaler() # 클래스 선언
MM.fit(df[cols]) # 데이터 인풋
df[cols] = MM.transform(df[cols]) # 변환
3) RobustScaler = Standardization (표준화)의 변형 버전
★ mean(평균)을 빼고 std(표준편차)를 나누는 대신, median(중위값)을 빼고 IQR(Q3-Q1)을 나누어 표준화
★ ★ 기존 StandardScaler는 mean과 std의 특성상 "이상치"의 영향을 많이 받으나,
RobustScaler는 그렇지 않음

from sklearn.preprocessing import RobustScaler
RS = RobustScaler() # 클래스 선언
RS.fit(df[cols]) # 데이터 인풋
df[cols] = RS.transform(df[cols]) # 변환
4) MaxAbsScaler = Normalization (정규화)의 변형 버전
★ 절대값이 0~1사이, 즉 (-1 ~ 1 사이의 수직선에 모든 값이 놓이게 하는 개념)
★ ★ 기존 MinMaxScaler처럼 "이상치"의 영향력 큼
★ ★ ★ "(해당 값) / (절대값의 최대값)" 의 비율로 계산되어 항상 min값이 -1 또는 0을 갖는다고 보기 힘듬
** 반면 MinMaxScaler는 절대값 0이 있던 없던 간에 무조건 최소값이 0

from sklearn.preprocessing import MaxAbsScaler
MA = MaxAbsScaler() # 클래스 선언
MA.fit(df[cols]) # 데이터 인풋
df[cols] = MA.transform(df[cols]) # 변환
5★) Normalize() = 각 독립변수(컬럼)간의 상대적인 크기를 조정하기 위한 Scaler
★ 기존의 것들은 전부 기준점이 하나의 컬럼이었지만, 기준이 하나의 줄이 되는 Scaler
★ 독립 변수간에 각 비중이 알맞게 수정됨
from sklearn.preprocessing import Normalizer
Nl = Normalizer() # 클래스 선언
Nl.fit(df[cols]) # 데이터 인풋
df[cols] = Nl.transform(df[cols]) # 변환
★ ★ 즉, 시점이 1, 금액이 2 일때랑 시점이 2, 금액이 4 일때 같은 수치로 조정해주는 표준화
3. 차원축소
★ 샘플 데이터
# 와인 데이터 불러오기
import pandas as pd
from sklearn.datasets import load_wine
dataset = load_wine()
data = pd.DataFrame(dataset.data, columns=dataset.feature_names)
차원축소란 무엇인가? 흔히들 공간을 일컫어 3차원이라고 지칭한다. 예시로 x, y, z 좌표만으로 우주의 위치를 지칭하기도 한다. 지구도 공간인데 왜 위도와 경도 2차원적으로 설명하냐면, 지구의 지각을 이루는 공간을 2차원화 시킨 지도에서 위치를 표기하기 위해 사용되는 것이다. 즉, 3차원->2차원 우리 입장에서 지구 내핵과 맨틀, 지각을 구분하는 z값은 큰 의미가 없기 때문에 사용하지 않는 것이다. 이것이 바로 차원축소의 개념과 비슷하다.
고차원을 저차원으로 바꾸는 것, 데이터에서는 overfitting문제를 해결하기 위해 사용한다.
1) 주성분분석 : PCA(Principal Component Analysis)
단계별로 공분산이 최대가 되는 축을 찾아 한 차원씩 축소하는 과정을 거친다. 이를 통해 다차원을 목표 차원까지 지속적으로 수정한다.
why : 공분산이 커야 데이터들 간의 차이점이 명확해져, 정보손실을 가장 최소화 시킬 수 있다.

★ 주성분분석을 하기 위해 스케일링을 해야하는 이유
1. 변수 간의 단위 차이 보정 : 큰 범위를 가지는 값일수록 많은 중요성이 부여될 수 있다.
2. 고유값 분해의 안정성 향상 : 차원을 축소하는 과정에서 안정성을 높이기 위해서이다.
3. 결과의 해석 용이성 : 성분의 계수들이 원래 변수들과 어떤 관계에 있는지 더 쉽게 해석할 수 있다.
★ ★ PCA의 종류
1. PCA(일반PCA)
2. IncrementalPCA(점진적 PCA)
3. SparsePCA(희소 PCA)
4. KernelPCA(커널 PCA)

2번 Incremental PCA는 일반 PCA에 대비 미니배치로 메모리의 효율성을 늘리고, 추가 및 업데이트가 용이하도록 변경한 것을 말한다.
3번 Sparse PCA의 설명을 보면 "데이터가 매우 크고 희소할 때, 변수의 수가 많을 때"라는 말이 애매할 수 있는데, 이는 줄의 수는 많으나 0 또는 Null값이 많은 경우를 뜻한다.
4번 Kernel PCA는 일반 PCA는 선형관계와 관련이 있는 공분산을 기준점을 잡는 만큼, 선형 이외의 관계를 지닌 데이터의 축소 방법을 말한다.
# 스탠다드 스케일링
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
data = scaler.fit_transform(data)
df = data.copy()
# PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=2) # 2차원!
df = pca.fit_transform(df)
df = pd.DataFrame(df)
# IncrementalPCA
from sklearn.decomposition import IncrementalPCA
ipca = IncrementalPCA(n_components=2)
df_transformed = ipca.fit_transform(df)
df_transformed = pd.DataFrame(df_transformed)
# SParcesPCA
from sklearn.decomposition import SparsePCA
spca = SparsePCA(n_components=2)
df_transformed = spca.fit_transform(df)
df_transformed = pd.DataFrame(df_transformed)
# KernelPCA
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(n_components=2)
df_transformed = kpca.fit_transform(df)
df_transformed = pd.DataFrame(df_transformed)
여기서 n_componets는 목표 차원을 의미한다.
2) SVD(Singular Value Decomposition) 특이값 분해

행렬개념을 활용하는 기법으로, 분해하여 특이값 중 작은 것들을 제거하는 방향으로 불필요한 정보를 제거해나간다고 생각하면 좋다. SVD기법은 특히 이미지 데이터에서 유용한 데 유용한 이유는 다음과 같다.

from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=2)
df_transformed = svd.fit_transform(df)
df_transformed = pd.DataFrame(df_transformed)
언뜻 보았을 때, 나는 사용자가 어떤 것이 불필요한 지 판단 못하는 상황에서 SVD의 방식이 더 유효하지 않나 생각했으나, Chat-gpt의 답변은 반대였다. 즉, 판단할 수 없기 때문에 함부러 제거하지 못하고 그 정보손실을 최소화 시키는 PCA방식이 선호된다는 것이었다. AI를 만들기 위해 기본적인 이해가 선행되지 않는다면 이렇듯 큰 오류를 범할 수 있음을 많이 느낄 수 있었다.
'Python > Scikit-learn' 카테고리의 다른 글
| Sklearn의 기초 - 자연어 처리(CountVectorizer, TfidfVectorizer) (0) | 2023.11.29 |
|---|---|
| Sklearn의 기초 - 군집화(비계층적, 계층적) (0) | 2023.11.27 |
| Scikit-learn의 기초 - 회귀(선형, 라쏘, 릿지, 랜덤포레스트, XGBoost) (0) | 2023.11.25 |
| Scikit-learn의 기초 - 분류(의사결정나무, 랜덤포레스트, xgboost) (2) | 2023.11.23 |
| Scikit-learn의 기초 - 지도학습 데이터 split(학습, 검증용), 교차 검증 (0) | 2023.11.22 |



